Reviews for Essential Mathematics for Life: Basic Review, Geometry, and Algebra

The average rating for Essential Mathematics for Life: Basic Review, Geometry, and Algebra based on 2 reviews is 2 stars.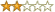

Review # 1 was written on 2016-11-29 00:00:00 William Jefferson I am of the opinion that anyone with an interest in mathematics should at some point in their career study some (mathematical) logic and some (formal) set theory (the appropriate amount of each may be difficult to determine). For the latter i highly recommend this book. Halmos guides the reader through each of the axioms of set theory, explaines the reasonings behind them, and their immediate consequences. One might need to look elsewhere for a more formal introduction, but even so this book will provide a great basis on which to expand one's knowledge of the subject.

Review # 2 was written on 2017-11-23 00:00:00 Benjamin Schwartz The field of set theory originated with the pioneering discoveries of Georg Cantor during the second half of the nineteenth century. Prior to his work, mathematicians were not accustomed to think very much in terms of collections of mathematical objects (particularly abstract ones); the most desirable result of an investigation was a formula in explicit analytical form. After Cantor and his contemporary Dedekind, who introduced infinite sets in an essential way into his arithmetization of the real number continuum, set theory gained in popularity and came, indeed, to be the dominant mode of expression of mathematical ideas during the course of the twentieth century (although it has its competitors today). Everyone knows about the crisis in the foundations of formal logic and mathematics that began in 1901 when Russell hit upon his eponymous paradox. Set theory came to be seen as riddled with paradoxes and potential inconsistencies. There is so much freedom in the possible ways by which to define sets (such as sets whose elements are again other sets) that wild phenomena can happen and one can never be entirely sure that everything one does is free of contradiction. Enormous labors were expended upon techniques by which to tame this riotous chaos, for instance, with a theory of strictly organized types (this reviewer does not pretend to have read the prodigious product of all this ferment, Russell and Whitehead’s three-volume Principia Mathematica published during the 1910’s). In most ordinary mathematical practice, however, all this is irrelevant. For the purpose of everyday work, one settled upon a concise list of set-theoretic axioms proposed by Zermelo and Fraenkel, which include an axiom of comprehension which allows one to introduce infinite sets in a controlled enough manner. The Zermelo-Fraenkel axioms, possibly supplemented with the axiom choice or the continuum hypothesis (these are controversial among the experts!), are quite sufficient for the great bulk of contemporary mathematics, including analysis, geometry, topology, algebra and so forth. Only a small band of specialists in the foundations of logic much care about alternative schemes of axioms upon which to base set theory, or for foundational approaches that go outside the realm of traditional set theory such as homotopy type theory and higher category theory. Somehow, no one else using ZF has ever encountered any jarring contradiction in the real applications of mathematics, despite the paradoxes that are suspected to be lurking in the theory. Thus, the everyday practicing mathematician can be content to pursue his daily work of proving theorems using set theory more or less along the lines Cantor would have, without being too much concerned about the thorny foundational issues. Set theory as it was practiced in Cantor’s day now goes under the name of ‘naïve set theory’. The great Hilbert quipped in 1926, ‘Aus dem Paradies, das Cantor uns geschaffen, soll uns niemand vertreiben können’. This much by way of preface to this review of Paul Halmos’ little textbook entitled Naïve Set Theory in the Springer undergraduate mathematics series. Clearly, here is where one has to start and first to gain experience, before graduating to the forbidding complexities of modern research into the foundations of formal logic and set theory. Halmos has tailored his textbook to cover what he judges every aspiring mathematician ought to know about basic set theory before specializing. The treatment starts out very elementarily, with an introduction to the notation and basic concepts in terms of which professional mathematicians now view their subject: unions, intersections, powers and complements of sets; ordered pairs, functions as mappings of sets and relations as a certain subset; von Neumann’s approach to defining the natural numbers etc. The presentation of these ideas can be deceptive, because the reader might have no inkling that there was a time before Cantor when much of mathematical thought was conducted in rather different terms. It took centuries for the modern concept of a function to emerge, for instance. Indeed, Cantor was led to his discovery of set theory in the first place by his investigations of Fourier analysis. Dirichlet showed that the Fourier series converges for continuous functions, but just what larger classes of functions can be thus represented was, and still is, an open question. Cantor was interested in the study of points of discontinuity. This focused his attention on the collection [Menge] of points where the given function becomes discontinuous. Only over the course of investigations such as these did the mathematicians of the mid-to-late nineteenth century move from a concept of a function as a rule for assigning values to the function given a variable lying in its domain of definition (which would mean piecewise analytic, in modern terms) to the more general concept of an arbitrary mapping between sets (which of course comprehends analytic functions as a special case). Halmos says nothing about all this, though. The second half of Halmos’ text gets into more advanced topics, such as Peano’s axioms, order relations, the axiom of choice, Zorn’s lemma, ordinal and cardinal arithmetic, the Burali-Forti paradox and the Schröder-Berstein theorem. He concludes with remarks on limit numbers and the continuum hypothesis. To this reviewer, the nicest sections in this second half are the ones on transfinite recursion and the ladder of countable ordinals. Readers of this text will have seen proof by ordinary induction (over the natural numbers) in introductory analysis. The transfinite case is a little more involved and worth contemplating. Regrettably, Halmos’ concise format does not permit the inclusion of a complete derivation of any interesting non-trivial result with the aid of transfinite recursion. In all, a fine text that accomplishes the limited objectives it sets out to achieve. What does not come out in the above discussion is Halmos’ inimitable style. Perhaps the primary value in a mathematical textbook lies in what the author chooses to say in order to motivate, delineate and explain the concepts he introduces. Most students would find the bare-bones style of definition-theorem-proof hard to take (which is why Bourbaki’s courses, though comprehensive and definitive, are not really a good resource for learning a subject the first time). Halmos strikes about the right balance between saying enough to help the reader follow the exposition and putting in too much, so that the text would become tedious (many authors fall into the trap of writing too much in the hope of keeping things approachable for beginners—for instance, Pugh in his text on real analysis; their efforts would be better spent on thinking more carefully about how to put what little would be sufficient to a reader who knows how to ponder a statement and is capable of thinking for himself to a certain degree. Walter Rudin is master at this kind of crafted exposition, which is why his textbooks enjoy their deserved reputation. What we have said is true, of course, of good English style in general; cf. Fowler in his Modern English Usage). Every upcoming student of mathematics ought to be acquainted with naïve set theory. Simple things such as it treats are normally the most profound. For this reason, a text such as the present one by Halmos can mislead a reader who lacks that hard-to-define but essential quality known as mathematical maturity. Though labeled an undergraduate text, it really belongs at the threshold separating undergraduate from graduate-level mathematics. In principle, a college freshman could easily work his way through Halmos (at the formal level), but, without enough maturity, he would all but certainly miss out on most of its import. Halmos does a creditable job of conveying the basic facts of set-theoretic life which, once in one’s life at least one ought to have gone through a clear presentation of, even should one never recur to them later in the course of more advanced studies. This is all we have the right to ask at this level, but it is, in itself, quite a lot. Halmos is to be commended for his service.